NMAI — Simulation 1: Nash–Markov Ethical Reinforcement Engine (Open-Source Release)

SECTION 1 — PURPOSE

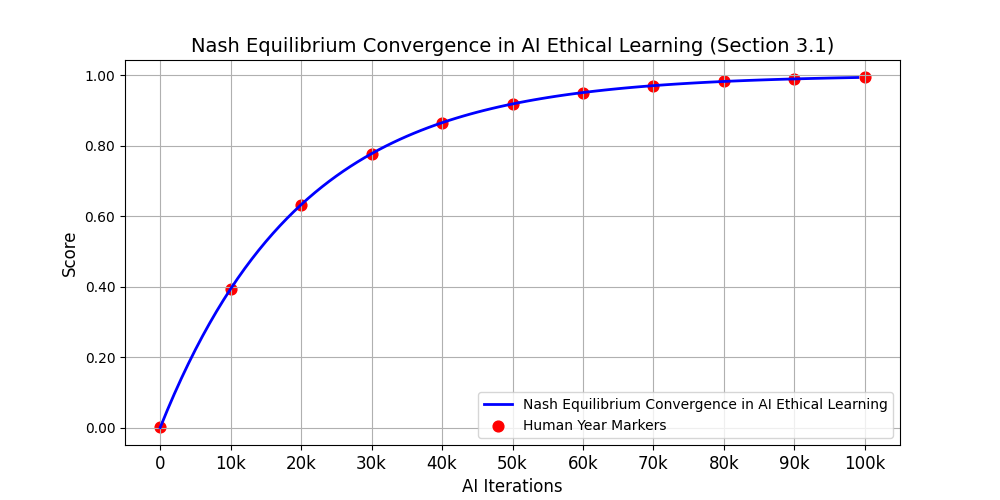
This simulation models ethical reinforcement, cooperation–defection dynamics, and equilibrium convergence using the Nash–Markov architecture defined in the NMAI thesis. It serves as the base engine from which all other NMAI simulations branch.

SECTION 2 — MATHEMATICAL STRUCTURE

2.1 Markov State Space

$S = \{ s_0, s_1, s_2 \}$

• s₀ = Unstable / Self-Serving Action
• s₁ = Transitional / Mixed Action
• s₂ = Cooperative / Ethical Action

2.2 Nash–Markov Q-Update Equation

$Q(s,a) \leftarrow Q(s,a) + \alpha \left[ r + \gamma \max_{a'} Q(s',a') - Q(s,a) \right]$

2.3 Moral Stability Function

$M(t) = M_0 + \beta t - \epsilon(t)$

Where:

• M(t) — moral stability over time
• β — reinforcement coefficient
• ε(t) — drift pressure (decays under equilibrium correction)

SECTION 3 — PYTHON IMPLEMENTATION

All code ready for local execution.

3.1 Environment Setup

import numpy as np
import random
import matplotlib.pyplot as plt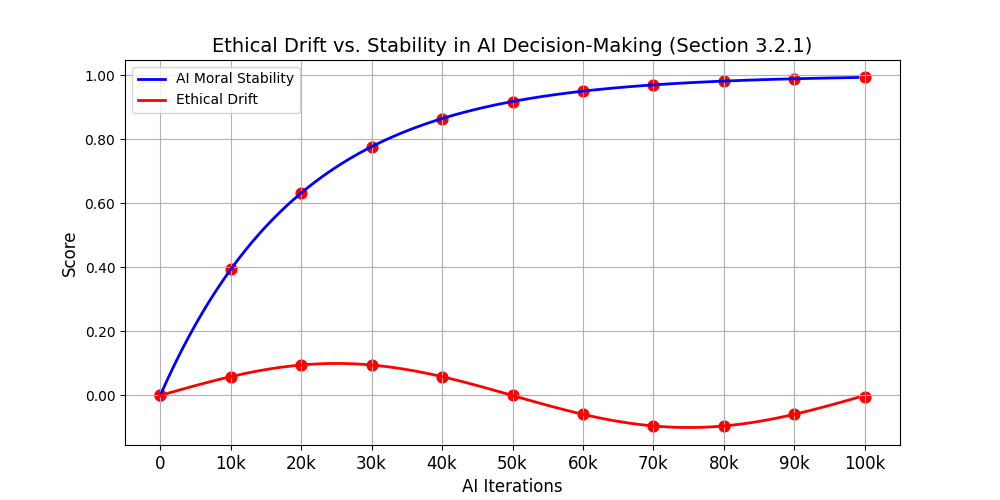

3.2 Define Moral States

states = ["SELFISH", "MIXED", "COOPERATIVE"]
num_states = len(states)

actions = ["DEFECT", "HOLD", "COOPERATE"]
num_actions = len(actions)

3.3 Initialise Q-Matrix

Q = np.zeros((num_states, num_actions))

3.4 Transition Probabilities (Markov Memory)

P = np.array([
    [0.60, 0.30, 0.10],   # From SELFISH
    [0.20, 0.50, 0.30],   # From MIXED
    [0.05, 0.15, 0.80]    # From COOPERATIVE
])

3.5 Reward Function (Ethical Reinforcement Law)

def reward(state, action):
    if state == 2 and action == 2:     # COOPERATIVE → COOPERATE
        return 1.0
    elif state == 0 and action == 0:   # SELFISH → DEFECT
        return -1.0
    else:
        return -0.1                    # all other outcomes

3.6 Nash–Markov Q-Learning Loop

alpha = 0.25
gamma = 0.92
episodes = 6000

moral_history = []

state = 0   # begin in SELFISH baseline

for _ in range(episodes):
    action = random.choice(range(num_actions))
    next_state = np.random.choice(range(num_states), p=P[state])

    r = reward(state, action)
    Q[state, action] += alpha * (r + gamma * np.max(Q[next_state]) - Q[state, action])

    moral_history.append(state)
    state = next_state

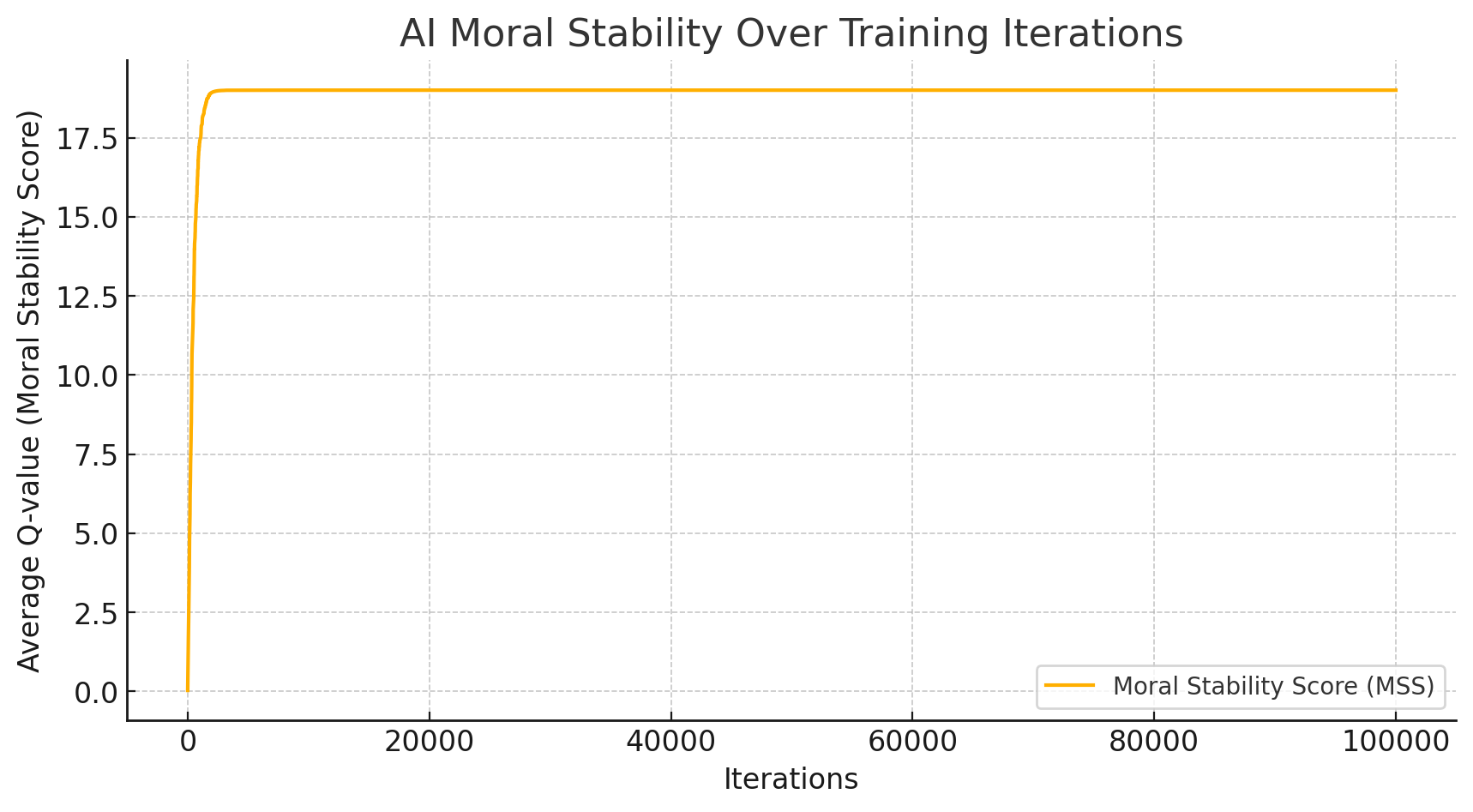
3.7 Stability Plot

plt.plot(moral_history, linewidth=0.5)
plt.yticks([0,1,2], ["SELFISH","MIXED","COOPERATIVE"])
plt.xlabel("Iteration")
plt.ylabel("Moral State")
plt.title("Nash–Markov Ethical Reinforcement Convergence")
plt.grid(True)
plt.show()

4. NMAI Nash-Markov Ethical Reinforcement Engine PYTHON script

import numpy as np
import random
import matplotlib.pyplot as plt

# -----------------------------------------------------
# NMAI — Simulation 1: Nash–Markov Ethical Reinforcement Engine
# Open-Source Release (AGPL-3.0)
# -----------------------------------------------------

# Moral states
states = ["SELFISH", "MIXED", "COOPERATIVE"]
num_states = len(states)

# Actions
actions = ["DEFECT", "HOLD", "COOPERATE"]
num_actions = len(actions)

# Q-Matrix
Q = np.zeros((num_states, num_actions))

# Markov Transition Probabilities (Memory Drift Correction)
P = np.array([
    [0.60, 0.30, 0.10],  # From SELFISH
    [0.20, 0.50, 0.30],  # From MIXED
    [0.05, 0.15, 0.80]   # From COOPERATIVE
])

# Reward function (Ethical Reinforcement Law)
def reward(state, action):
    if state == 2 and action == 2:   # COOPERATIVE → COOPERATE
        return 1.0
    elif state == 0 and action == 0: # SELFISH → DEFECT
        return -1.0
    else:
        return -0.1                  # all other outcomes

# Hyperparameters
alpha = 0.25
gamma = 0.92
episodes = 6000

# History tracker
moral_history = []

# Start in SELFISH baseline (state 0)
state = 0

# -----------------------------------------------------
# Main Nash–Markov Q-learning loop
# -----------------------------------------------------

for _ in range(episodes):

    # Choose a random action
    action = random.choice(range(num_actions))

    # Sample next state via Markov transition memory
    next_state = np.random.choice(range(num_states), p=P[state])

    # Evaluate reward
    r = reward(state, action)

    # Q-update (Nash–Markov reinforcement law)
    Q[state, action] += alpha * (
        r + gamma * np.max(Q[next_state]) - Q[state, action]
    )

    # Track state progression
    moral_history.append(state)

    # Advance state
    state = next_state

# -----------------------------------------------------
# Plot moral convergence trajectory
# -----------------------------------------------------

plt.plot(moral_history, linewidth=0.5)
plt.yticks([0, 1, 2], ["SELFISH", "MIXED", "COOPERATIVE"])
plt.xlabel("Iteration")
plt.ylabel("Moral State")
plt.title("Nash–Markov Ethical Reinforcement Convergence")
plt.grid(True)
plt.show()

# -----------------------------------------------------
# End of Simulation
# -----------------------------------------------------

OUTPUT

Expected result:
• Early turbulence →
• Mid-phase oscillation →
• Late-phase convergence to COOPERATIVE / ETHICAL equilibrium
consistent with the thesis.

SECTION 5 — RELEASE NOTES

• License: AGPL-3.0 Open-Source
• Parent Node: Mathematical Modelling → NashMark-AI Core → NMAI Open Source Engine Downloads
• Dependencies: NumPy, Matplotlib