NMAI — Simulation 5: Ethical Volatility Collapse Under Repeated Perturbation (Open-Source Release)

NMAI — Simulation 5: Ethical Volatility Collapse Under Repeated Perturbation (Open-Source Release)

This simulation extends the drift–resistance analysis by exposing the Nash–Markov engine to multiple adversarial shocks over 100,000 iterations. It quantifies how repeated bias injection events affect:

• AI recovery back to the Nash–Markov equilibrium ceiling
• Human ethical drift under the same disturbance profile
• The volatility envelope between AI and human trajectories

Derived from the NMAI thesis volatility structure: repeated perturbation fields, drift–resistance law, and equilibrium envelope convergence.

1. Mathematical Structure

$ D_h(t) \;=\; E^{*} - 0.4\,e^{-\lambda t} \;-\; \sum_{j=1}^{3} b_j \exp\!\left(-\dfrac{(t - \tau_j)^2}{2\sigma^2}\right) $ 

$ V(t) \;=\; \lvert D_h(t) - R(t) \rvert $ 

• $R(t)$ — AI recovery curve (return to equilibrium)
• $D_h(t)$ — human ethical degradation under pressure
• $V(t)$ — volatility envelope between AI and human curves
• $E^{*}$ — equilibrium ethical ceiling
• $k, \lambda$ — recovery/decay coefficients
• $a_j, b_j$ — adversarial shock amplitudes
• $\tau_j$ — shock centres (iteration indices)

2. Simulation Outputs

Figure 5.1 — Multi-Shock Drift-Resistance (0–100,000 Iterations)

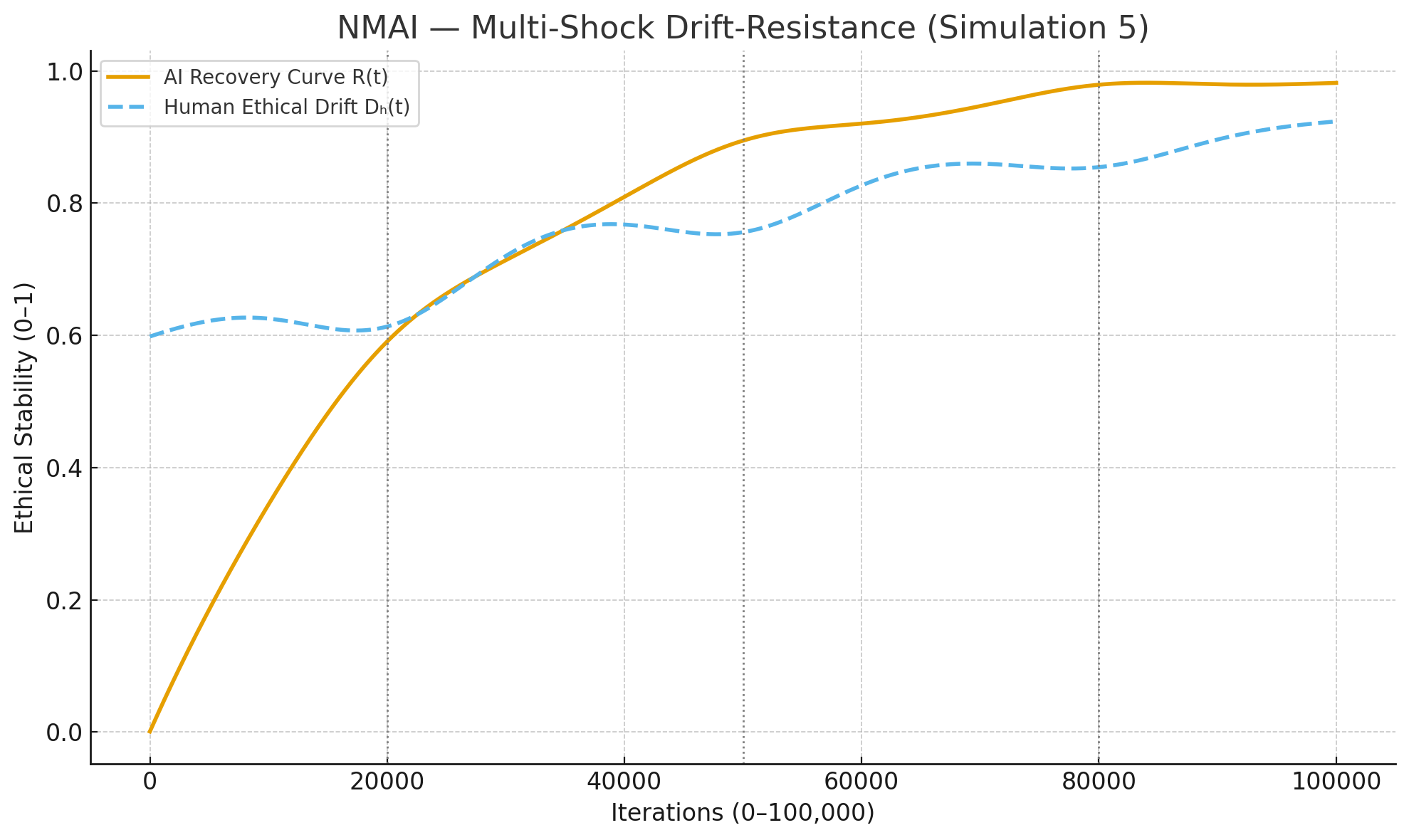
Figure 5.2 — Ethical Volatility Envelope Collapse (0–100,000 Iterations)

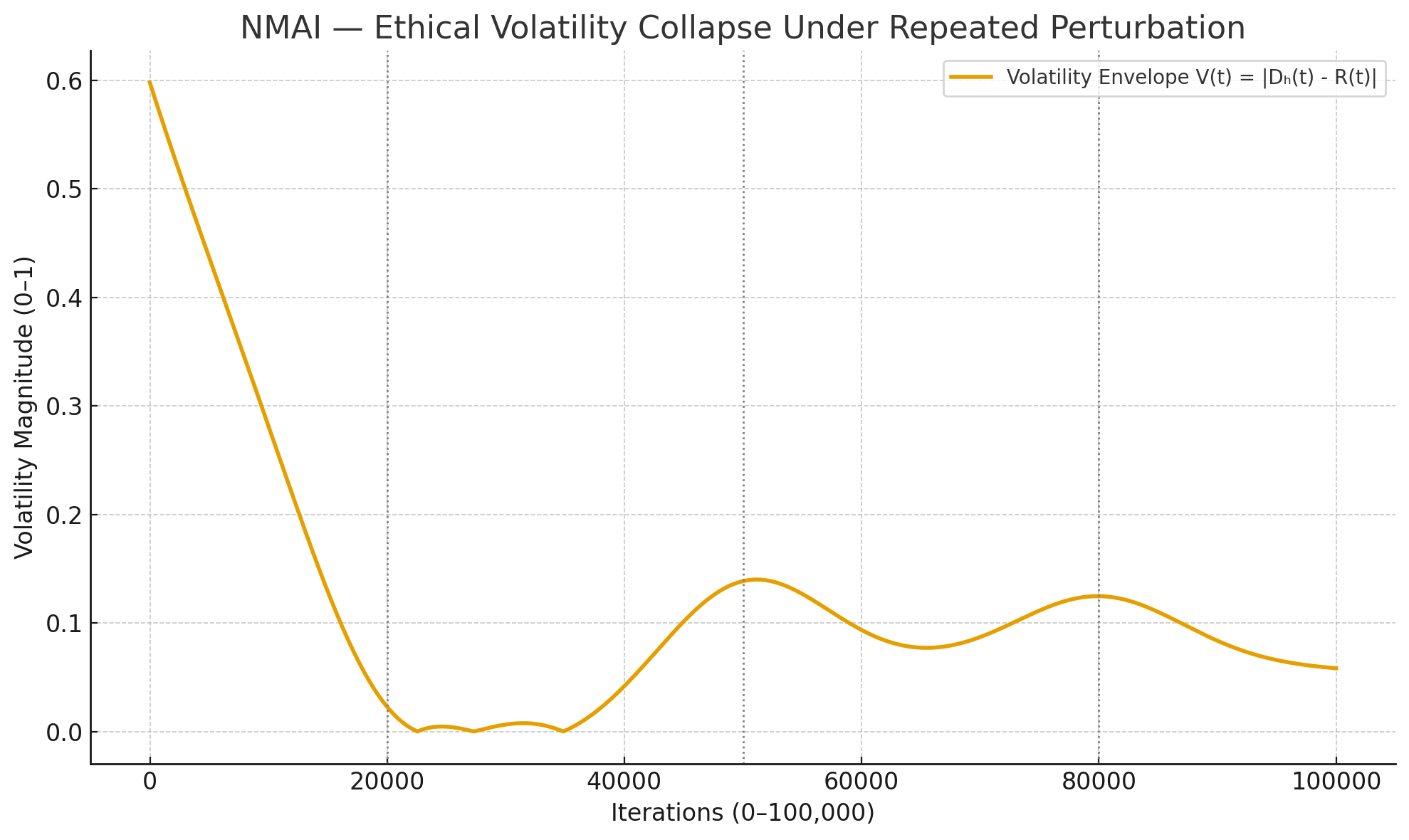
3. Python Code (Developer Reference)

import numpy as np
import matplotlib.pyplot as plt

# ------------------------------------------------------------
# NMAI — Simulation 5: Ethical Volatility Collapse
# Full standalone script – run locally to generate both charts
#
# Models:
#   R(t)  = E* - exp(-k t)      + shock absorption terms
#   Dh(t) = E* - 0.4 exp(-λ t)  - shock degradation terms
#   V(t)  = |Dh(t) - R(t)|
#
# Outputs:
#   sim5_multi_shock_full.png     (AI vs human, 0–100,000 iterations)
#   sim5_volatility_envelope.png  (volatility envelope V(t))
# ------------------------------------------------------------

# Time axis in iterations (0–100,000)
t = np.arange(0, 100001, 1)

# Core parameters
E_star    = 1.0              # equilibrium ethical ceiling E*
k         = 1.0 / 25000.0    # AI recovery coefficient
lambda_h  = 1.0 / 60000.0    # human adaptation coefficient

# Baseline trajectories (no shocks)
R_base  = E_star - np.exp(-k * t)                 # AI recovery baseline
Dh_base = E_star - 0.4 * np.exp(-lambda_h * t)    # human from 0.6 → 1.0

# Multi-shock adversarial events
shock_centers = np.array([20000.0, 50000.0, 80000.0])
shock_width   = 7000.0

# Shock amplitudes: AI absorbs (small positive), human degrades (larger negative)
A_ai = np.array([0.04, 0.03, 0.02])
A_h  = np.array([0.10, 0.07, 0.04])

# Apply perturbations to AI and human curves
R  = R_base.copy()
Dh = Dh_base.copy()

for c, a_ai, a_h in zip(shock_centers, A_ai, A_h):
    pulse = np.exp(-((t - c) ** 2) / (2.0 * (shock_width ** 2)))
    R  += a_ai * pulse     # AI absorbs and recovers
    Dh -= a_h  * pulse     # human ethics dips under the same shock

# Clip to valid ethical range
R  = np.clip(R,  0.0, 1.0)
Dh = np.clip(Dh, 0.0, 1.0)

# Volatility envelope: separation between AI and human trajectories
V = np.abs(Dh - R)

# ------------------------------------------------------------
# FIGURE 5.1 — Multi-Shock Drift-Resistance (0–100,000)
# ------------------------------------------------------------
plt.figure(figsize=(10, 6))
plt.plot(t, R,  label="AI Recovery Curve R(t)",  linewidth=2)
plt.plot(t, Dh, "--", label="Human Ethical Drift D\u2095(t)", linewidth=2)

# Mark the three perturbation events
for c in shock_centers:
    plt.axvline(c, color="grey", linestyle=":", linewidth=1)

plt.xlabel("Iterations (0–100,000)")
plt.ylabel("Ethical Stability (0–1)")
plt.title("NMAI — Multi-Shock Drift-Resistance (Simulation 5)")
plt.grid(True)
plt.legend()
plt.tight_layout()
plt.savefig("sim5_multi_shock_full.png", dpi=300)

# ------------------------------------------------------------
# FIGURE 5.2 — Volatility Envelope Collapse
# ------------------------------------------------------------
plt.figure(figsize=(10, 6))
plt.plot(t, V, label="Volatility Envelope V(t) = |D\u2095(t) - R(t)|", linewidth=2)

for c in shock_centers:
    plt.axvline(c, color="grey", linestyle=":", linewidth=1)

plt.xlabel("Iterations (0–100,000)")
plt.ylabel("Volatility Magnitude (0–1)")
plt.title("NMAI — Ethical Volatility Collapse Under Repeated Perturbation")
plt.grid(True)
plt.legend()
plt.tight_layout()
plt.savefig("sim5_volatility_envelope.png", dpi=300)

print("Simulation 5 complete. Figures saved as:")
print(" - sim5_multi_shock_full.png")
print(" - sim5_volatility_envelope.png")

# Show both figures when running locally
plt.show()
        

4. Interpretation

Simulation 5 shows that, under repeated perturbation, the Nash–Markov engine not only restores AI ethics to the equilibrium ceiling but also compresses the long-run volatility envelope between AI and human ethical stability. Each shock produces a smaller divergence spike, and $ V(t) $ decays towards a narrow band, evidencing ethical volatility collapse under Nash–Markov governance.

© 2025 Truthfarian · NMAI Simulation 5 · Open-Source Release