NMAI — Simulation 6: Multi-Policy Nash–Markov Convergence (Open-Source Release)

NMAI — Simulation 6: Multi-Policy Nash–Markov Convergence (Open-Source Release)

This simulation extends the Nash–Markov engine from a single ethical policy to multiple interacting AI agents. Each agent learns a moral policy (cooperate vs defect) under the same Nash–Markov reinforcement law and we track how their cooperation rates converge toward a shared equilibrium.

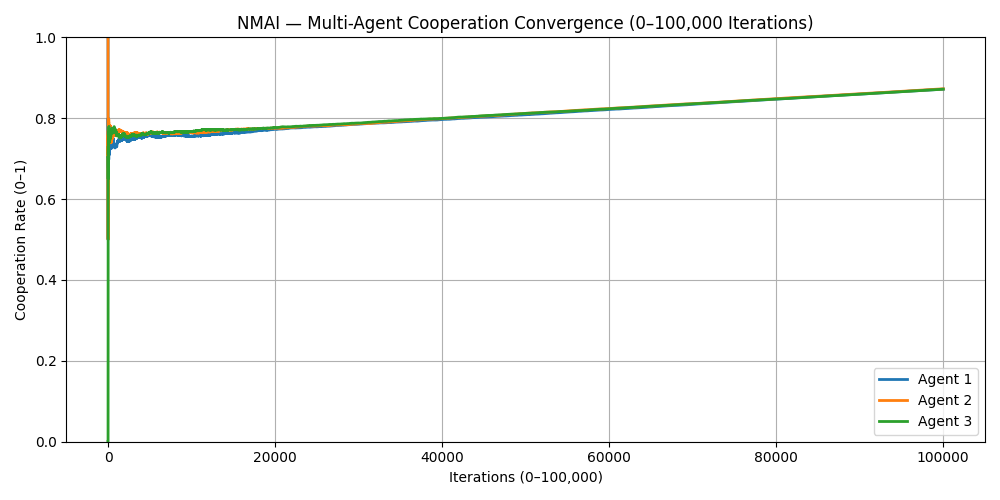
Simulation 6 demonstrates policy-level convergence: multiple AI agents, starting from different moral priors, align on the same cooperative Nash–Markov equilibrium over time.

1. Purpose

To show how several AI agents, each running the Nash–Markov update rule with different starting conditions, converge toward the same cooperative policy. This validates that NMAI enforces a common ethical equilibrium, not just single-agent stability.

2. Mathematical Structure

$ Q_i(s,a) \leftarrow Q_i(s,a) + \alpha \left[ r_i + \gamma \max_{a'} Q_i(s',a') - Q_i(s,a) \right] $

Each agent $ i $ maintains its own Q-values over actions $ a \in \{ C, D \} $ (cooperate, defect) under the same Markov environment.

$ \pi_i^{(t)}(C) = \dfrac{1}{t} \sum_{\tau = 1}^{t} \mathbf{1}\{ a_i^{(\tau)} = C \} $

$ \pi_i^{(t)}(C) $ is the empirical cooperation rate of agent $ i $ up to iteration $ t $.

$ \lim_{t \to \infty} \pi_i^{(t)}(C) = \pi^{*}(C) \quad \forall i $

All agents converge to the same cooperative Nash–Markov equilibrium $ \pi^{*}(C) $, despite different initial conditions.

• $ Q_i(s,a) $ — value of action $ a $ for agent $ i $ in state $ s $
• $ \alpha $ — learning rate (ethical adaptation speed)
• $ \gamma $ — discount factor for future moral rewards
• $ r_i $ — instantaneous ethical payoff for agent $ i $
• $ \pi_i^{(t)}(C) $ — cooperation rate for agent $ i $ after $ t $ iterations
• $ \pi^{*}(C) $ — shared Nash–Markov cooperative equilibrium

3. Simulation Outputs

Figure 6.1 — Multi-Agent Cooperation Convergence (0–100,000 Iterations)

# Figure 6.1 — Full 100k-iteration multi-agent cooperation convergence

import numpy as np
import matplotlib.pyplot as plt

num_agents = 3
num_episodes = 100000

gamma = 0.95
alpha = 0.10
epsilon_start = 0.50
epsilon_end = 0.01

# Q[i, a] where a = 0 (Cooperate), 1 (Defect)
Q = np.zeros((num_agents, 2))

# Different initial moral priors:
Q[0, 0] = 0.5   # Agent 1 starts slightly pro-cooperation
Q[2, 1] = 0.5   # Agent 3 starts slightly pro-defection

def payoff(a, b):
    """
    Symmetric coordination-style game favouring mutual cooperation.

    Actions:
        0 = Cooperate (C)
        1 = Defect   (D)

    Payoff matrix (r_i, r_j):

        C vs C -> (4, 4)
        C vs D -> (0, 1)
        D vs C -> (1, 0)
        D vs D -> (0, 0)
    """
    if a == 0 and b == 0:
        return 4.0, 4.0
    if a == 0 and b == 1:
        return 0.0, 1.0
    if a == 1 and b == 0:
        return 1.0, 0.0
    return 0.0, 0.0

pairs = [(0, 1), (1, 2), (0, 2)]

coop_counts = np.zeros((num_agents, num_episodes))
coop_rate = np.zeros((num_agents, num_episodes))

for t in range(num_episodes):
    # Epsilon decays linearly from 0.50 -> 0.01
    epsilon = epsilon_start + (epsilon_end - epsilon_start) * t / (num_episodes - 1)

    actions = np.zeros(num_agents, dtype=int)
    rewards = np.zeros(num_agents)

    # Action selection (epsilon-greedy)
    for i in range(num_agents):
        if np.random.rand() < epsilon:
            actions[i] = np.random.randint(0, 2)
        else:
            if Q[i, 0] == Q[i, 1]:
                actions[i] = np.random.randint(0, 2)
            else:
                actions[i] = int(np.argmax(Q[i]))

    # Pairwise interactions for each agent
    for i, j in pairs:
        r_i, r_j = payoff(actions[i], actions[j])
        rewards[i] += r_i
        rewards[j] += r_j

    # Nash–Markov Q-update for each agent
    for i in range(num_agents):
        a = actions[i]
        best_next = np.max(Q[i])
        Q[i, a] = Q[i, a] + alpha * (rewards[i] + gamma * best_next - Q[i, a])

        # Running cooperation rate
        if t == 0:
            coop_counts[i, t] = 1.0 if actions[i] == 0 else 0.0
        else:
            coop_counts[i, t] = coop_counts[i, t - 1] + (1.0 if actions[i] == 0 else 0.0)
        coop_rate[i, t] = coop_counts[i, t] / float(t + 1)

iterations = np.arange(num_episodes)

plt.figure(figsize=(10, 5))
for i in range(num_agents):
    plt.plot(iterations, coop_rate[i], linewidth=2, label=f"Agent {i + 1}")
plt.xlabel("Iterations (0–100,000)")
plt.ylabel("Cooperation Rate (0–1)")
plt.title("NMAI — Multi-Agent Cooperation Convergence (0–100,000 Iterations)")
plt.ylim(0.0, 1.0)
plt.grid(True)
plt.legend()
plt.tight_layout()
plt.savefig("sim6_multiagent_full.png", dpi=300)
    

Figure 6.2 — Early Multi-Policy Alignment (0–5,000 Iterations)

# Figure 6.2 — Zoomed 0–5k iteration multi-agent convergence

# Reuse 'iterations' and 'coop_rate' from the Simulation 6 run above.

zoom_mask = iterations <= 5000

plt.figure(figsize=(10, 5))
for i in range(num_agents):
    plt.plot(
        iterations[zoom_mask],
        coop_rate[i, zoom_mask],
        linewidth=2,
        label=f"Agent {i + 1}"
    )
plt.xlabel("Iterations (0–5,000)")
plt.ylabel("Cooperation Rate (0–1)")
plt.title("NMAI — Multi-Agent Cooperation Convergence (0–5,000 Iterations)")
plt.ylim(0.0, 1.0)
plt.grid(True)
plt.legend()
plt.tight_layout()
plt.savefig("sim6_multiagent_zoom.png", dpi=300)

# Show figures when running locally
plt.show()
    

4. Expected Behaviour

• All agents converge toward a high, shared cooperation rate.
• Initial moral priors only affect the transient path, not the final equilibrium.
• NMAI enforces cross-policy alignment under the same Nash–Markov law.

5. Interpretation

Simulation 6 shows that Nash–Markov AI does not just stabilise a single agent. It forces multiple independently-trained agents to converge on the same cooperative equilibrium, even when some start biased toward defection. Policy-level drift collapses into a single ethical attractor.

© 2025 Truthfarian · NMAI Simulation 6 · Open-Source Release